In the 1600's, calculators were not commonplace. Worse, many did not have access to education. Yet, like today, math was everywhere. Thus, there was a need for ordinary people to be able to complete computations. Enter John Napier.

Napier was a Scottish landowner who saw math as a hobby. He was devoted to taking care of the Gartness estate and used his talents as an inventor to excel at his duties. Napier applied math everywhere, including to improve the land by applying scientific thought to agriculture.

While most famous for his invention of the logarithm, Napier had many extraordinary contributions including decimal notation for fractions, and what we are here for: Napier's Bones.

Solving the problem of allowing anyone to compute easily, Napier's Bones is often considered the first practical calculator. When you think about the first calculator, you may automatically imagine a large and complex device, but surprisingly, Napier's Bones is easy to make and fit in the palm of your hand.

Invented in 1615, Napier used his brilliant mathematical mind along with his talents as an inventor to construct a remarkably insightful and easy-to-use device that can multiply, divide, and even find square roots quite simply.

This makes Napier's Bones ideal for young students. Not only are the bones fun to play with, students need only the ability to add and subtract to harness the power of the device.

So how does Napier's Bones work? Consider the standard multiplication table. On its face, it is a 10-by-10 square (our table below adds an additional "0" column) constructed by skip counting that allows us to reference the product of two values with factors of 10 or less. But the multiplication table is so much more! The periodic table of numbers, every bit of our multiplication table is hiding secrets, connections, and beautiful relationships between values.

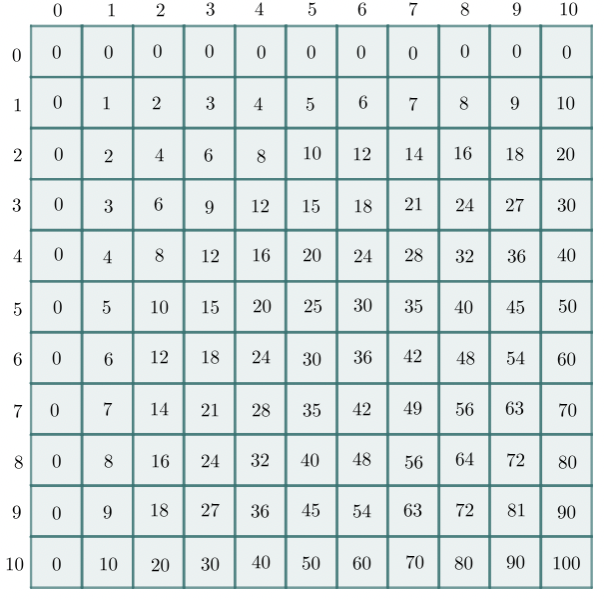
Recall our activity Table Mash Up from MathBait™ Multiplication Part 3. In this lesson, students explored the multiplication table from different perspectives. This is just what John Napier did. Using his deep understanding of mathematics, he broke apart the table and began rearranging its columns.

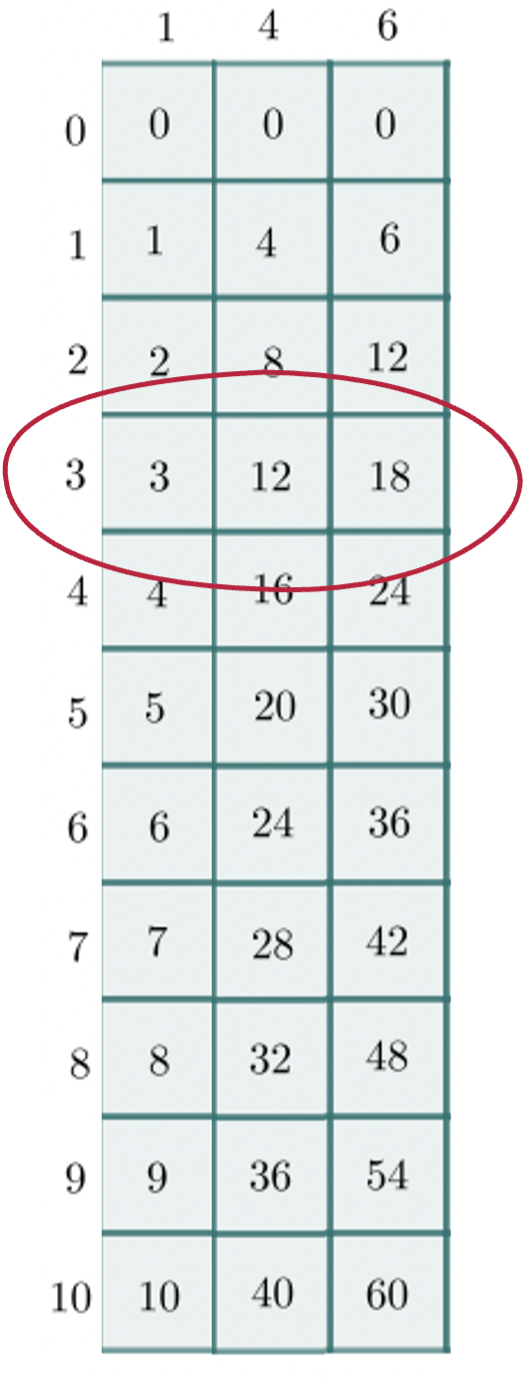
Taking the columns for 1, 4, and 6, Napier could now place these next to each other and examine their relationship. If he focused on the third row he noticed that each value was exactly the third multiple of his column headers (in this case 1×3, 4×3, and 6×3). The resulting number was 31218 which had no practical use, but Napier had a deep understanding of mathematics. If he wanted to multiply 146×3, the standard steps would be to find 3×6, 3×4, and 3×1, exactly the values that lay in front of him.

Taking into account place value, the number 31218 could be thought of as (31)(21)(8) where each value in parentheses corresponds to the place value the number would be applied to. Adding together the numbers in each place value led to (3+1)(2+1)(8)=(4)(3)(8)=438 (note the juxtaposition used here refers to place value rather than multiplication).

Grab your calculator! The value of 146×3 is precisely 438. 

Amazing! Napier's rearrangement of the multiplication table is the magic behind his bones.

John Napier constructed a powerful manipulative. Each rod consists of the multiples of each digit and thus, in essence, are simply columns of the multiplication table. Rather than jotting down each product, Napier split each cell into two places: tens and ones. This allowed his rods, or "bones", to create joints, and rather than carrying over as in the standard algorithm, the joints are already situated so that each place value lines up for easy addition.

Playing with Napier's Bones can help students strengthen their single-digit fluency while also helping them to better understand multi-digit multiplication. This is a great way to introduce students to multi-digit multiplication as they will build confidence as they easily compute the product of very large numbers. In addition, students will begin to build an intuitive understanding of place value that will transfer directly to partial products or the standard algorithm.

John Napier. MacTutor Archives. Available at https://mathshistory.st-andrews.ac.uk/Biographies/Napier/.